Bu yazıda birden fazla sensör barındıran IMU(Inertial measurement unit) kartlarının içinde bulunan akselerometrenin çalışma prensibini inceleyeceğiz.
Temel olarak aşağıdaki önemli başlıklardan bahsedeceğim:
- Akselerometre ne ölçer?
- Sensörlerden okuduğumuz analog değeri dijitale (ADC) nasıl çeviririz? Okunan bu değerleri nasıl yorumlarız?
Bu yazıda matematiği olabildiğince hafif tutmaya çalıştım. Eğer temel trigonometrik işlemeleri biliyorsanız yazıyı rahatlıkla anlayabilir ve mantığı anladığınız için de tüm geliştirme platformunda (Arduino kartları, Atmel çipleri, PIC, Raspberry Pi v.b.) bunu uygulayabilirsiniz. Genellikle insanlar IMU sensörler için çok karmaşık matematik işlemler olduğuna inanırlar. (Kalman filitresi gibi karmaşık FIR or IIR filitreleri, Parks-McClellan filitreleri…vb) Bu yöntemleri araştırabilirsiniz ama bir anda karışık matris işlemleri ile karşılaşırsınız. Bu yüzden öncelikle basit bir matematikle, çalışma yöntemlerini ve sensör değerlerini neden ve nasıl işlediğimizi anlamamız gerekir. Bu karmaşık işlemlerin asıl sebebi, akselerometrede okunan değerin çok gürültülü olmasıdır. Bu sensörler, yapısı gereği titreşimlere ve gürültüye çok duyarlıdır ve ham değerleri çok anlamsızdır. Bu matematik işlemlerini kullanarak sensörden gelen ham değerleri aslında olması gereken değerlere yaklaştırmaya çalışırız.
Akselerometre
Akselerometrenin çalışma mantığını anlamak için içinde top olan küp şeklinde bir kutu hayal edelim.
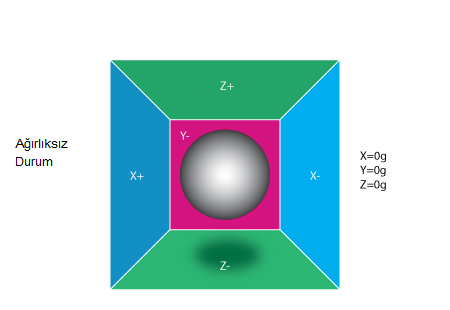
Başta bu kutuyu uzayda kabul edelim. Uzayda topun pozisyonunu bozacak herhangi bir yerçekimi veya dışsal kuvvet olmasın. Top hareketsiz halde küpün ortasında dursun. Yukarıdaki resimde gördüğünüz gibi kutunun yüzeyinde her eksenin ismi yazılı (kutunun içine bakmak için Y+ eksenini çıkardım). Şimdi tüm duvarların basınca duyarlı olduğunu düşünün. Eğer kutumuzu aniden g ivmesiyle sola çekersek topumuz X- eksenindeki duvara çarpar ve biz topun duvara yaptığı baskı kuvvetini ölçmüş oluruz. Bu durumda çıkış değeri X ekseninde -1g olarak ölçülür.
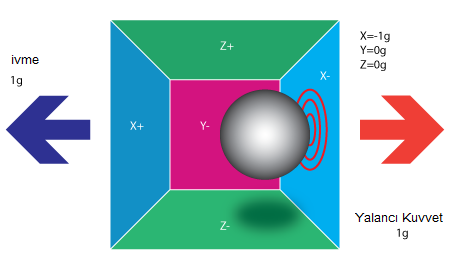
Yani şekilde anlaşıldığı gibi akselerometre uygulanan ivmenin ters doğrultusunu ölçer. Bu kuvvet yalancı kuvvet (eylemsizlik kuvveti) olarak adlandırılır. Böylelikle asıl ivme değerini dolaylı bir yoldan ölçeriz (tabi ki bu bizim modelimiz için geçerli, bu ölçüm gerçek hayatta herhangi bir etkiyle değişiklik gösterebilir). Bu kuvvet sadece ivme kuvvetiyle oluşur ama bir sonraki örnekte bu kuvvetin sadece ivme kuvveti ile oluşmadığını göreceğiz.
Eğer modelimizi dünyaya taşırsak, şekildeki gibi topumuz küpün içinde g değerinde Z- duvarına baskı uygular.
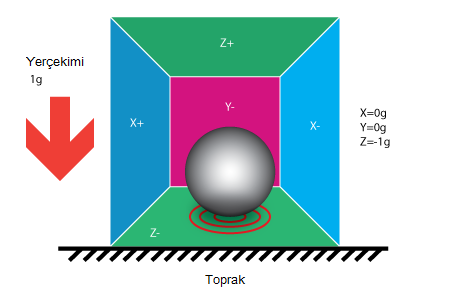
Küp hareket etmiyorsa, sürekli Z ekseninde -1g büyüklüğünde değer okuruz. Duvara uygulanan baskı yerçekimi kuvvetinden kaynaklıdır. Sistemi başka tip kuvvetler de etkileyebilir, mesela topun metal olduğunu düşünün ve dışardaki bir mıknatıs, topu başka bir duvara baskı uygulatabilir. Bu akselerometreden okuduğumuz ham değerin aslında gerçek ivme değerleri olmadığını gösterir.
Bu modelleme bu sensörlerin nasıl çalıştığını ve iç yapısını açıklamaz. Bu modelleme akselerometrede oluşan problemlerin temelinin anlaşılmasını sağlar. Aslında içinde metal top bulunan ve eğim anahtarları denilen sensörler mevcuttur. Bu ilkel sensörler sadece bazı aralıklarda eğik olup olmadığını gösterebilir. Bu sensörlerin çalışma mantığı içinde civa olan bir tüpün 2 bacak arasına bazı eğimlerde kısa devre yapmasıdır.

Şimdiye kadar tek bir eksende ivme bilgisini analiz ettik. 3 eksenli akselerometreler 3 eksende de eylemsizlik kuvvetlerini ölçebilir. Şimdi küp modelimize geri dönelim ve modelimizi 45 derece sağa çevirelim. Şimdi topumuz 2 duvara aynı anda değecektir(-Z ve -X).
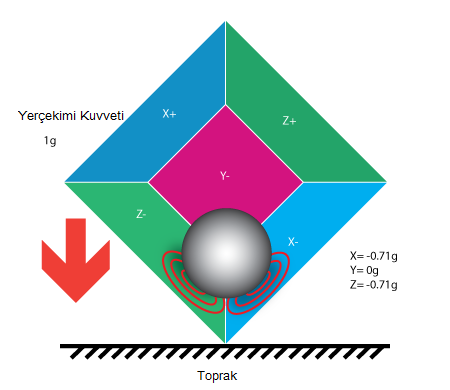
Resimdeki 0.71 öylesine bir değer değildir. Aslında √(1/2) nin yaklaşık değeridir. Bu durumu akselerometrenin diğer modeliyle tanıtmak daha açıklayıcı olacaktır.
Bir önceki modelimizde yerçekimi kuvvetini sabitleyip hayali kutumuzu döndürdük. Son iki örneğimizde, kuvvet vektörü sabitken iki farklı küp pozisyonunda elde edilen çıkışları inceledik. Akselerometrenin dış kuvvetlerle etkileşimini hesaplamamız için koordinat sistemi üstünde işlem yapmak daha kolaydır.
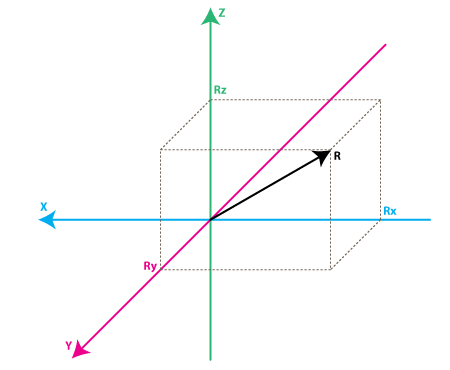
Şimdi yukarıdaki modellemeye bir göz atalım, eksen renklerine bakarak bir önceki modelden bir zihinsel geçiş yapalım. Sadece yeni modeldeki eksenlerin, önceki modeldeki kutunun aynı renkteki yüzeyine dik olduğunu düşünün. R vektörü akselerometrenin ölçtüğü kuvvet vektörüdür (bu yerçekimi veya eylemsizlik kuvveti veya ikisi de olabilir). Rx, Ry, Rz vektörleri R vektörünün X, Y, Z eksenine izdüşümleridir.
R^2 = Rx^2 + Ry^2 + Rz^2 (formülü ile açıklanabilir)
Bu olay basitçe 3 boyutlu pisagor teoremi ile açıklanabilir.
0.71 değerinin öylesine bir değer olmadığını hatırlarsak ve formülü önceki örnekte uygularsak
1^2 = (-√(1/2) )^2 + 0 ^2 + (-√(1/2))^2
R=1, Rx = -√(1/2), Ry = 0 , Rz = -√(1/2)
Rx, Ry, Rz aslında gerçek hayattaki akselerometre çıkışlarıdır ve çalışmalarımızı bu değerler üstünde yaparız.
Şimdi akselerometrenin bu bilgiyi bize nasıl verediği hakkında konuşalım. Bu yöntem genellikle iki çeşittir: dijital ve analog. Dijital akselerometreler bilgiyi I2C, SPI ve USART gibi seri haberleşme yöntemleri ile verirler. Analog akselerometreler belirli bir gerilim aralığında çıkış vereceğinden bunu dijitale çeviren ADC (Analog-to-digital converter) kullanılmalıdır. Konudan çok sapmamak için ADC hakkında çok açıklama yapmayacağım. Zaten arduinonun üstünde analog değer okuyabildiğimiz 10 bitlik ADC modülü vardır.
Bu yüzden 10 bit ADC ile basit bir örnek yapalım. ADC aşağıdaki değerleri verdiğini varsayalım.
AdcRx = 586
AdcRy = 630
AdcRz = 561
Her ADC modülün referans geriliminin 3.3V olduğunu var sayarsak (Arduino’da varsayılan olarak 5V’tur), 10 bit ADC ye gelen gerilimi şöyle hesaplayabiliriz:
VoltsRx = AdcRx * Vref / 1023
VoltsRx = 586 * 3.3V / 1023 =~ 1.89V
VoltsRy = 630 * 3.3V / 1023 =~ 2.03V
VoltsRz = 561 * 3.3V / 1023 =~ 1.81V
Her akselerometrede sıfır-g gerilimi vardır. Bu gerilimi IMU kartınızın datasheetini inceleyerek bulabilirsiniz. Bu gerilim 0g ye karşılık gelir. 0g gerilim seviyesini 1.65V varsayalım. Sıfır-g gerilimi ile gerilim değişimi şöyle ölçülür:
DeltaVoltsRx = 1.89V – 1.65V = 0.24V
DeltaVoltsRy = 2.03V – 1.65V = 0.38V
DeltaVoltsRz = 1.81V – 1.65V = 0.16V
Şuan akselerometreden okunan geirilim değerlerine sahibiz, hala g de değiliz. Nihai dönüşümler yapmak için akselerometrenin hassasiyetini bilmemiz gerekir. Hasasiyetin birimi mV/g dir. Hassasiyeti 478.5mV/g varsayalım. Kendi hassasiyet değerlerinizi akselerometrenizin datasheetlerini inceleyerek bulmalısınız. Nihai g değerini aşağıdaki formülle hesaplayabiliriz:
Rx = DeltaVoltsRx / Hassasiyet
Rx = 0.24V / 0.4785V/g =~ 0.5g
Ry = 0.38V / 0.4785V/g =~ 0.79g
Rz = 0.16V / 0.4785V/g =~ 0.33g
Tabiki tüm formülleri birleştirebilidim ama asıl mantığı anlamanız için tüm işlemleri adım adım yaptım. Asıl formül aşağıdaki gibidir:
Rx = (AdcRx * Vref / 1023 – VzeroG) / Hassasiyet
Ry = (AdcRy * Vref / 1023 – VzeroG) / Hassasiyet
Rz = (AdcRz * Vref / 1023 – VzeroG) / Hassasiyet
Eylemsizlik kuvvetini tanımlayan 3 tane parçamız var. Eğer yerçekiminden başka dış kuvvetler yoksa bunu yerçekiminin kuvvet vektörü doğrultusu varsayabiliriz. Eğer cihazın yere göre açısını hesaplamak istiyorsak bu vektörle Z ekseni arasındaki açıyı hesaplamalıyız. Aynı işlemi X ve Y eksenine yapabiliriz. Bu açıları hesaplamak için Rx, Ry ve Rz değerlerini hesapladık. Şimdi bir önceki akselerometre modelimize geri dönelim ve bazı ek gösterimler yapalım.
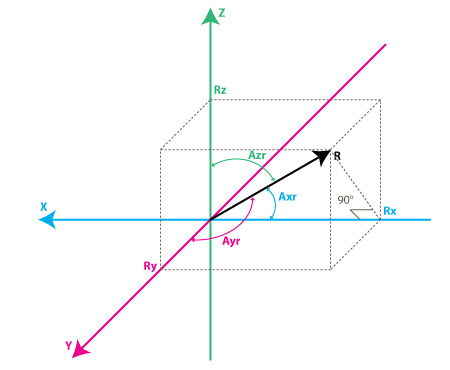
X, Y, Z eksenlerinin R vektörü ile yaptığı açıları AxR, Ayr ve Azr olarak tanımlayalım ve R ve Rx arasında bir dik üçgen hayal edelim.
cos(Axr) = Rx / R
cos(Ayr) = Ry / R
cos(Azr) = Rz / R
R = √( Rx^2 + Ry^2 + Rz^2)
Açıları arccos() fonksiyonu ile hesaplayalım
Axr = arccos(Rx/R)
Ayr = arccos(Ry/R)
Azr = arccos(Rz/R)
Bu formülleri akselerometre modelini en uzun yoldan açıklamak için kullandım. Uygulamanıza bağlı olarak bir kaç ara formüle daha ihtiyacınız olabilir. Bir sonraki yazıda jiroskop modelini inceleyeceğiz ve jiroskop ve akselerometre verilerini daha doğru şekilde eğim tahminleri almak için kombine edeceğiz.
Ama önce birkaç önemli nokta belirteyim:
cosX = cos(Axr) = Rx / R
cosY = cos(Ayr) = Ry / R
cosZ = cos(Azr) = Rz / R
Bu üçlü Direction cosine olarak adlandırılır ve birim vektör olarak temsil edilir.
√(cosX^2 + cosY^2 + cosZ^2) = 1
Bu özellik R vektörünün büyüklüğünü ölçmek için kullanılır. Eğer eylemsizlik vektörün yönüyle ilgileniyorsak, büyüklükleri sadeleştirmek hesaplamalarları kolaylaştırır.
Fransızca kaynak (PDF dosyası)








Çok faydalı oldu. Çok teşekkür ederiz. Allah sizden razı olsun.